Problemas con la definición de raíz cuadrada en los libros de texto de ESO y Bachillerato
Preparando mis clases para la asignatura de «Matemáticas orientadas a las enseñanzas académicas» de 4º de ESO he vuelto a encontrar el el libro de texto la siguiente definición de raíz cuadrada:
«La raíz cuadrada de un número real a es otro número real b que elevado al cuadrado da a»
Y añade la expresión:
dando a entender que si b es la raíz cuadrada de a escribiremos 
A mí nunca me ha terminado de convencer esta forma de definir las raíces cuadradas (o de índice par en general) de un número real. Les explico por qué, a ver si soy capaz de hacerme entender.
Demos por buena esta definición y la expresión con la doble implicación que describe la notación a utilizar. Consideremos un número real negativo, por ejemplo 
Como 
Llámenme pejiguero, pero me da a mí que un número negativo igual que otro positivo es una contradicción como la copa de un pino (salvo que este número sea el cero, que no es el caso).
Evidentemente puedo estar equivocado, así que si alguien ve algún error en mi razonamiento le ruego que me explique cuál es en los comentarios.
El problema se resolvería si se utilizase la siguiente definición:
«Dados dos números reales 
De esta forma, hasta donde yo alcanzo a ver, se resuelve la contradicción señalada, y de paso se introduce una forma clara de distinguir la raíz cuadrada positiva y negativa de un número real.
Podríamos, sin embargo, considerar que esta definición es demasiado abstracta para el alumnado de los primeros cursos de la ESO, y no sin razón. Por eso propongo esta otra manera de definir la raíz cuadrada para primero y segundo de la ESO, en la que mantenemos el rigor matemático a la vez que hacemos asequible el concepto (o, dicho de otra manera, explicamos las cosas poniéndolas lo más fáciles que sea posible pero sin tratar a nuestro alumnado como personas incapaces de hacer razonamientos complejos):
«Las raíces cuadradas de un número real 
Espero que les parezca adecuada, y si no, espero sus propuestas en los comentarios.
ACTUALIZACIÓN:
@gaussianos me ha recordado que ya habló de esto no hace mucho en su blog: https://www.gaussianos.com/cual-es-la-raiz-cuadrada-de-16/
Matemáticas de Secundaria: El teorema de Pitágoras
El teorema de Pitágoras es una propiedad que tienen los triángulos rectángulos, pero sólo la cumplen ellos, en los triángulos que no son rectángulos este teorema no se puede aplicar.
Recordemos para comenzar que un triángulo es rectángulo si uno de sus ángulos es recto. Los lados que forman el ángulo recto se llaman catetos, mientras que el opuesto a este ángulo se llama hipotenusa.
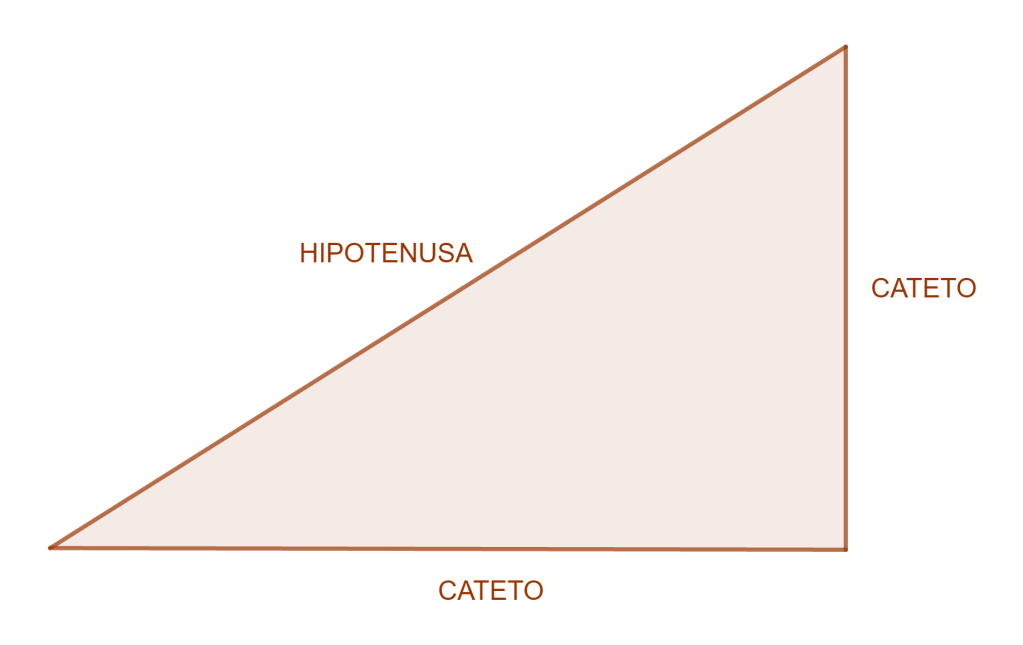
Si nos fijamos es fácil comprobar que la hipotenusa siempre es el lado más grande de los tres.
El teorema de Pitágoras dice que, si llamamos a y b a las longitudes de los catetos y h a la longitud de la hipotenusa,
Esto se cumple siempre en todos los triángulos rectángulos, sin excepción, y no se cumple en ninguno que no sea rectángulo.
Para los ejercicios necesitaremos utilizar la fórmula de otras dos maneras distintas:
· Si nos dan los dos catetos y nos piden la hipotenusa usaremos:
· Si nos dan la hipotenusa y un cateto, y nos piden el otro (da igual qué cateto sea), usaremos:
Aquí tenéis tres ejercicios como ejemplo:
Ejercicio 1: Comprueba que en este triángulo se cumple el teorema de Pitágoras.
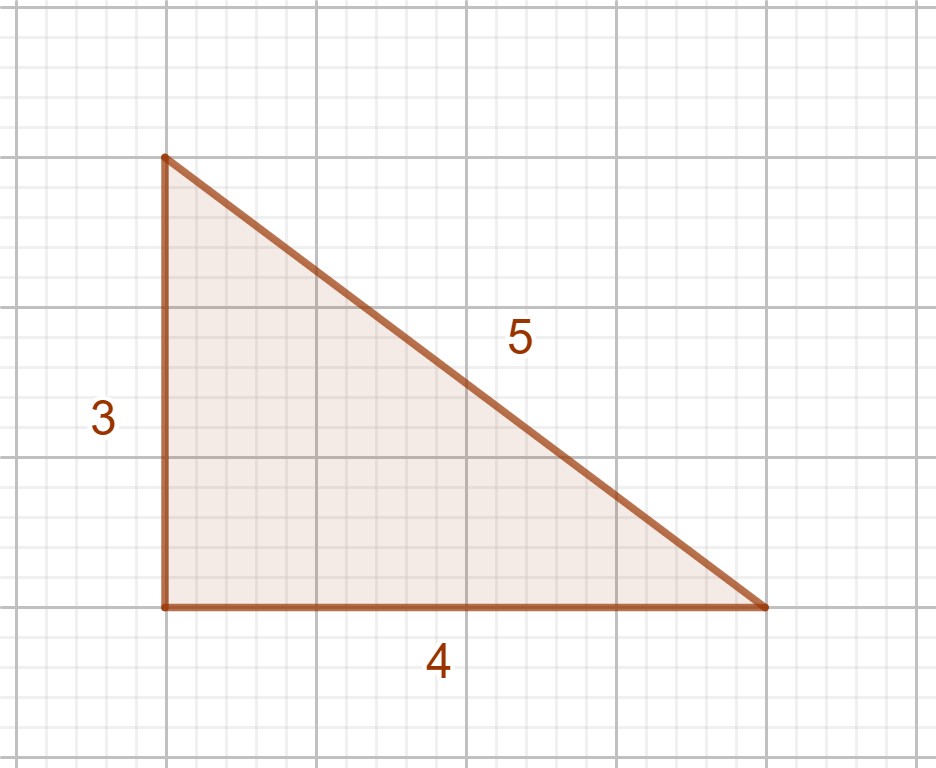
Tenemos que la hipotenusa vale 5 y los catetos 3 y 4. Si el teorema se cumple, esta expresión tiene que ser cierta:
Como 
y esto es verdadero, por lo que el teorema se cumple.
Ejercicio 2: Se quiere colocar un cable desde lo alto de una antena que mide 30 metros hasta un punto colocado a 15 metros de la base de la antena. ¿Cuánto debe medir el cable?
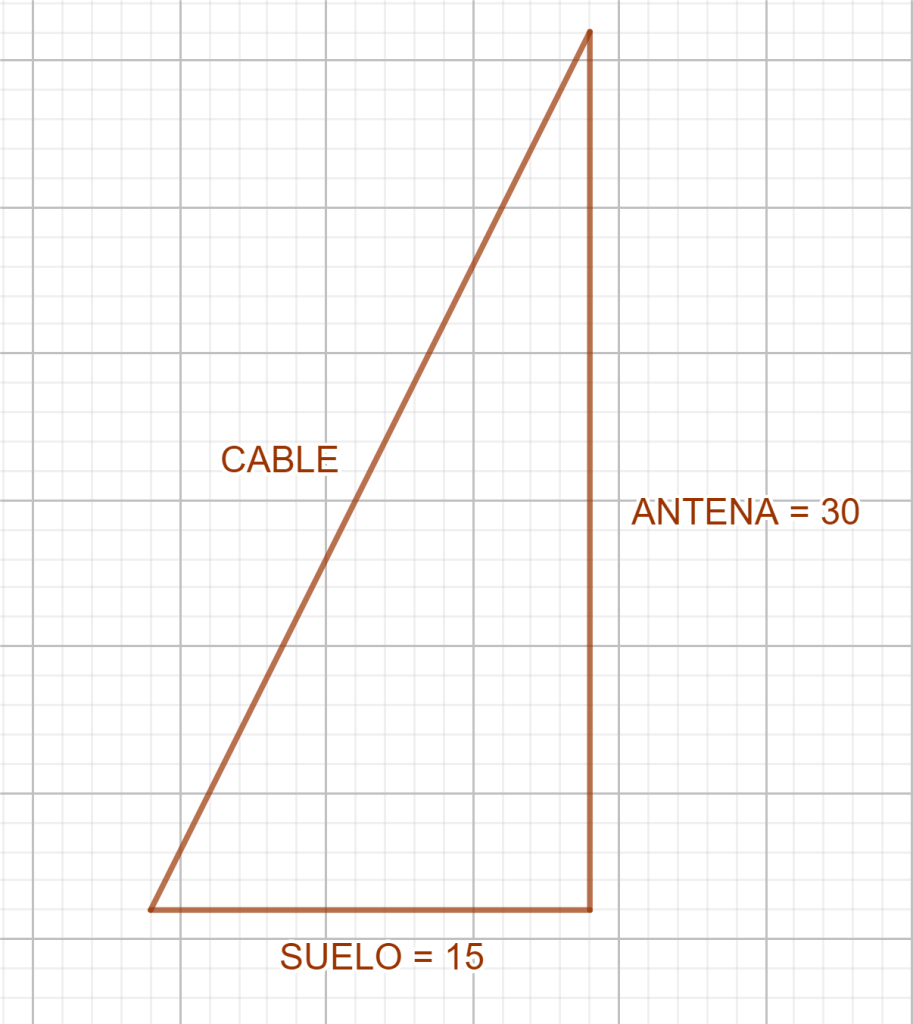
La antena, el cable y el suelo forman un triángulo rectángulo, donde la hipotenusa es precisamente el propio cable. Como conocemos los dos catetos utilizamos la segunda fórmula:
Con nuestra calculadora hacemos primero
Después hacemos la raíz cuadrada de 1125 y obtenemos la respuesta al problema:
El cable medirá aproximadamente 33 metros y 54 centímetros.
Ejercicio 3: Una parcela rectangular tiene un camino que cruza por su diagonal. Si el camino mide aproximadamente 18m y la parcela tiene 10 metros de ancho, ¿cuánto mide de largo?
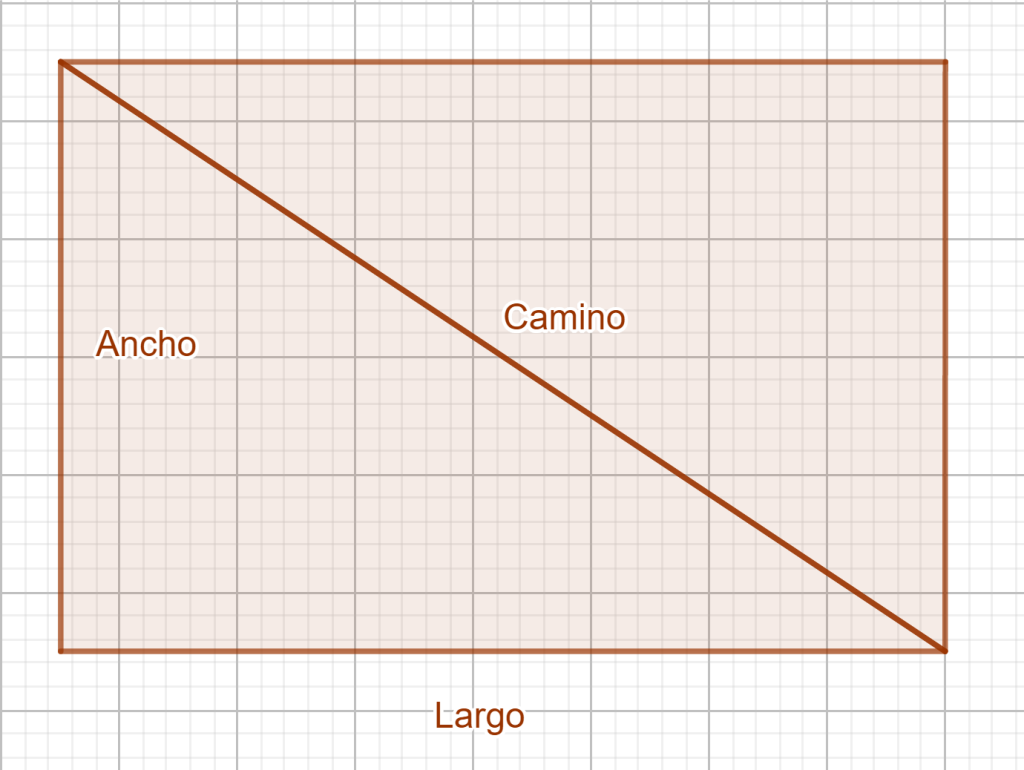
El camino que cruza a la parcela por su diagonal la divide en dos triángulos rectángulos iguales. Si nos quedamos con uno de ellos, conocemos su hipotenusa, que es el camino, y uno de los catetos (el ancho), por lo que la fórmula adecuada es la tercera:
El ancho de la parcela es, por tanto, 15 metros aproximadamente.
3º Académicas: Proporcionalidad y Geometría. Teorema de Tales.
Esta es una relación de actividades para el alumnado de 3º de ESO del IES Carmen Laffón que cursa la asignatura Matemáticas Orientadas a las Enseñanzas Académicas.
OBJETIVOS:
· Saber qué son polígonos semejantes.
· Conocer el Teorema de Tales.
· Saber cuándo dos triángulos están en posición de Tales.
· Saber cuándo dos triángulos son semejantes
MATERIAL:
· Todo lo que tienes que saber está en el apartado 6 del tema 6 de tu libro de texto, tendrás que leerlo varias veces. Copia los recuadros amarillos en tu cuaderno e intenta resolver los ejemplos por tí mismo.
· Revisa todo el material que tienes aquí a tu disposición y haz los ejercicios interactivos.
· Si los ejercicios interactivos no te salen bien, pregunta.
ACTIVIDADES:
· Cuando hayas trabajado bien todo lo anterior, realiza los ejercicios 49, 50, 51 y 52 de tu libro de texto.
Vídeo: Polígonos semejantes
Ejercicios interactivos de semejanza de polígonos:
Vídeo: Teorema de Tales
Ejercicios interactivos usando el teorema de Thales
Ocho ideas innovadoras para celebrar el día de Pi
Como ya sabrán, el próximo día 14 de marzo se celebra el día de Pi, y desde El máquina de Turing queremos compartir algunas de las mejores ideas que hemos encontrado en las redes para hacer de tu día de Pi una jornada inolvidable.
Sorprende a tus amigos, familiares y compañeros de trabajo y demuestra, al mismo tiempo, el amor por los números irracionales siguiendo estos ocho sencillos consejos.
1. Cómprate una tarta de tres chocolates de cinco centímetros de alto y veinticinco de diámetro. Cómetela. Pésate en una balanza de precisión.
Una explicación (más) del problema de Monty Hall
El problema del Monty Hall es un famoso ejemplo que ilustra muy bien lo poco que podemos fiarnos de nuestra intuición cuando se trata de calcular probabilidades. Aunque es bastante fácil encontrar descripciones y explicaciones muy buenas en la red, quiero aventurarme a proponer yo una que no sé si será mejor o peor que las demás, pero es la que a mí más me gusta. A ver qué les parece.
Como supongo ya sabrán, el problema consiste en un concurso en el que tenemos un presentador, un concursante y tres puertas cerradas. Detrás de cada una de ellas se esconde uno de estos tres objetos: una cabra, un coche y otra cabra. El concurso consiste en escoger una de las puertas, y el premio es lo que haya detrás de ella: o bien un coche, o bien una cabra. El presentador sabe en todo momento dónde está el coche, pero el concursante, obviamente, no. Si descartamos la posibilidad de que alguien prefiera quedarse con una de las cabras (nunca se sabe), el concurso se gana si detrás de la puerta escogida nos encontramos al coche y no un bóvido doméstico. Leer más →
El Máquina de Turing 
Comentarios recientes