Matemáticas de Secundaria: El teorema de Pitágoras
El teorema de Pitágoras es una propiedad que tienen los triángulos rectángulos, pero sólo la cumplen ellos, en los triángulos que no son rectángulos este teorema no se puede aplicar.
Recordemos para comenzar que un triángulo es rectángulo si uno de sus ángulos es recto. Los lados que forman el ángulo recto se llaman catetos, mientras que el opuesto a este ángulo se llama hipotenusa.
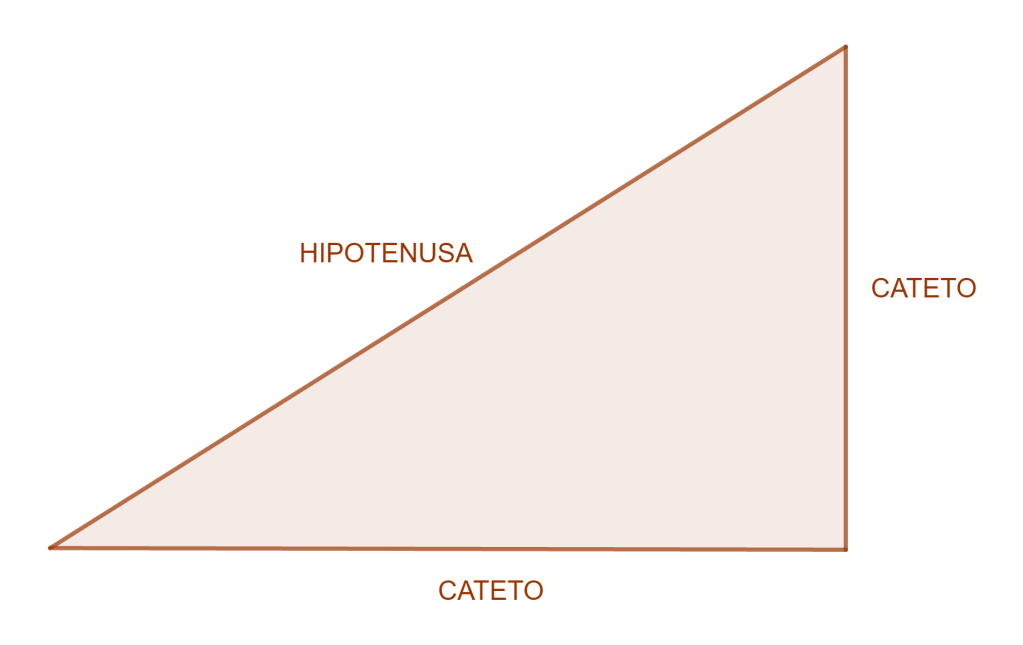
Si nos fijamos es fácil comprobar que la hipotenusa siempre es el lado más grande de los tres.
El teorema de Pitágoras dice que, si llamamos a y b a las longitudes de los catetos y h a la longitud de la hipotenusa,
Esto se cumple siempre en todos los triángulos rectángulos, sin excepción, y no se cumple en ninguno que no sea rectángulo.
Para los ejercicios necesitaremos utilizar la fórmula de otras dos maneras distintas:
· Si nos dan los dos catetos y nos piden la hipotenusa usaremos:
· Si nos dan la hipotenusa y un cateto, y nos piden el otro (da igual qué cateto sea), usaremos:
Aquí tenéis tres ejercicios como ejemplo:
Ejercicio 1: Comprueba que en este triángulo se cumple el teorema de Pitágoras.
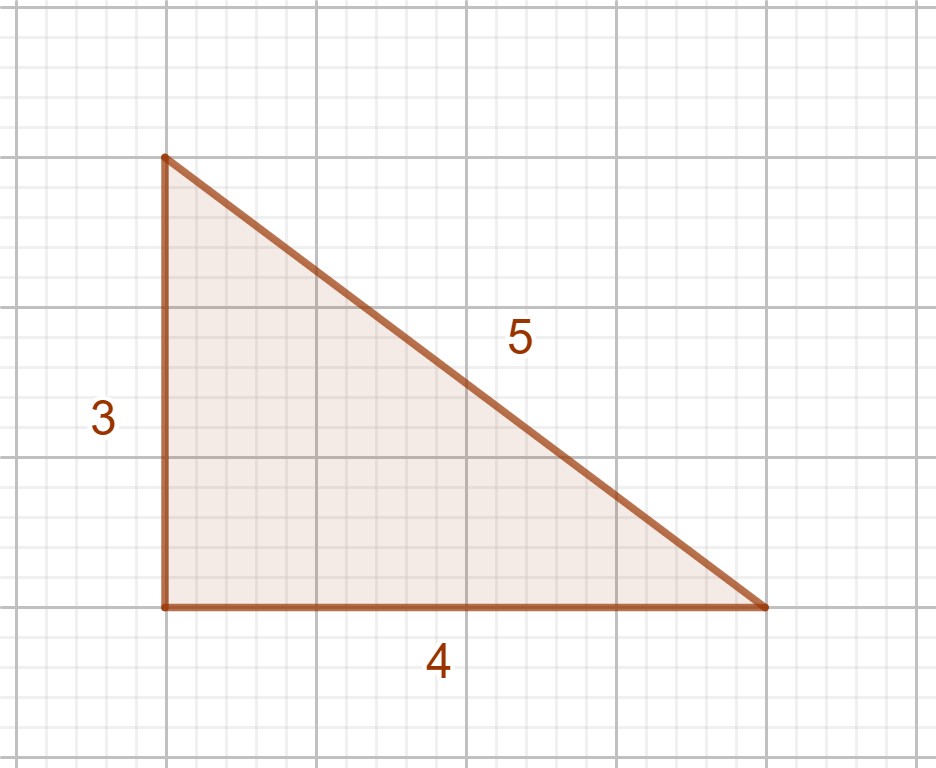
Tenemos que la hipotenusa vale 5 y los catetos 3 y 4. Si el teorema se cumple, esta expresión tiene que ser cierta:
Como 
y esto es verdadero, por lo que el teorema se cumple.
Ejercicio 2: Se quiere colocar un cable desde lo alto de una antena que mide 30 metros hasta un punto colocado a 15 metros de la base de la antena. ¿Cuánto debe medir el cable?
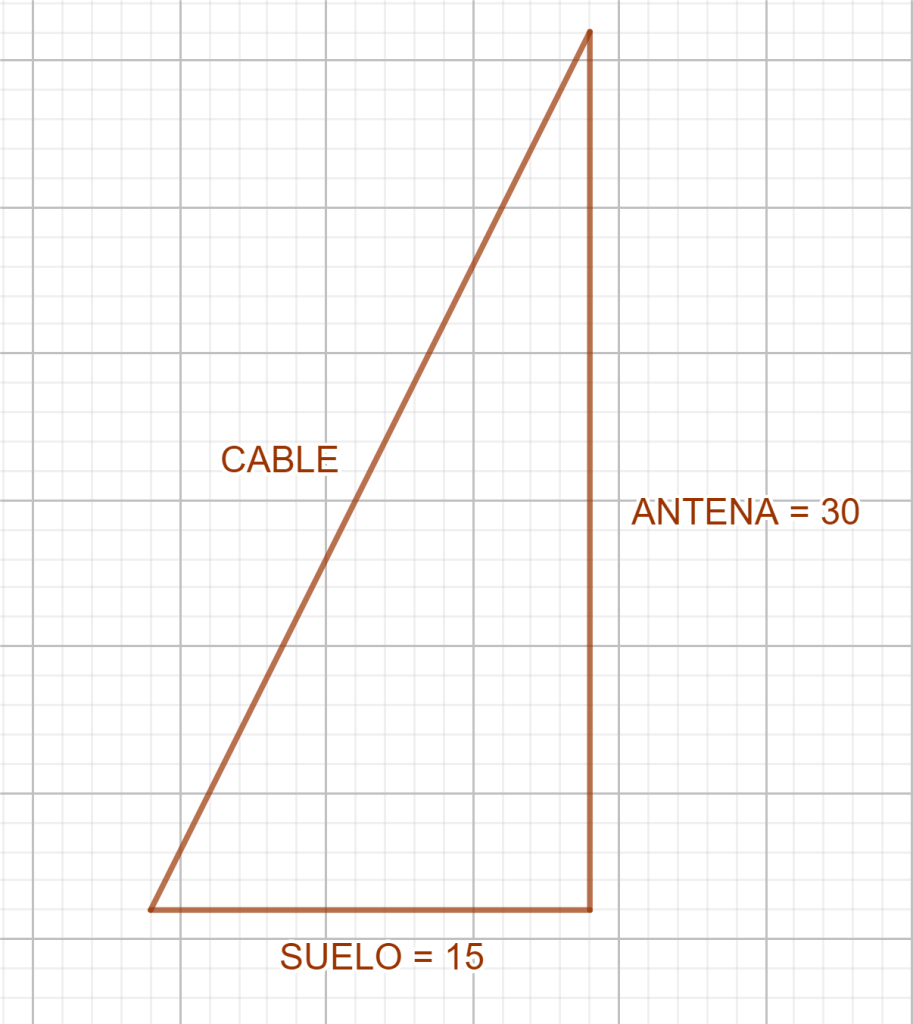
La antena, el cable y el suelo forman un triángulo rectángulo, donde la hipotenusa es precisamente el propio cable. Como conocemos los dos catetos utilizamos la segunda fórmula:
Con nuestra calculadora hacemos primero
Después hacemos la raíz cuadrada de 1125 y obtenemos la respuesta al problema:
El cable medirá aproximadamente 33 metros y 54 centímetros.
Ejercicio 3: Una parcela rectangular tiene un camino que cruza por su diagonal. Si el camino mide aproximadamente 18m y la parcela tiene 10 metros de ancho, ¿cuánto mide de largo?
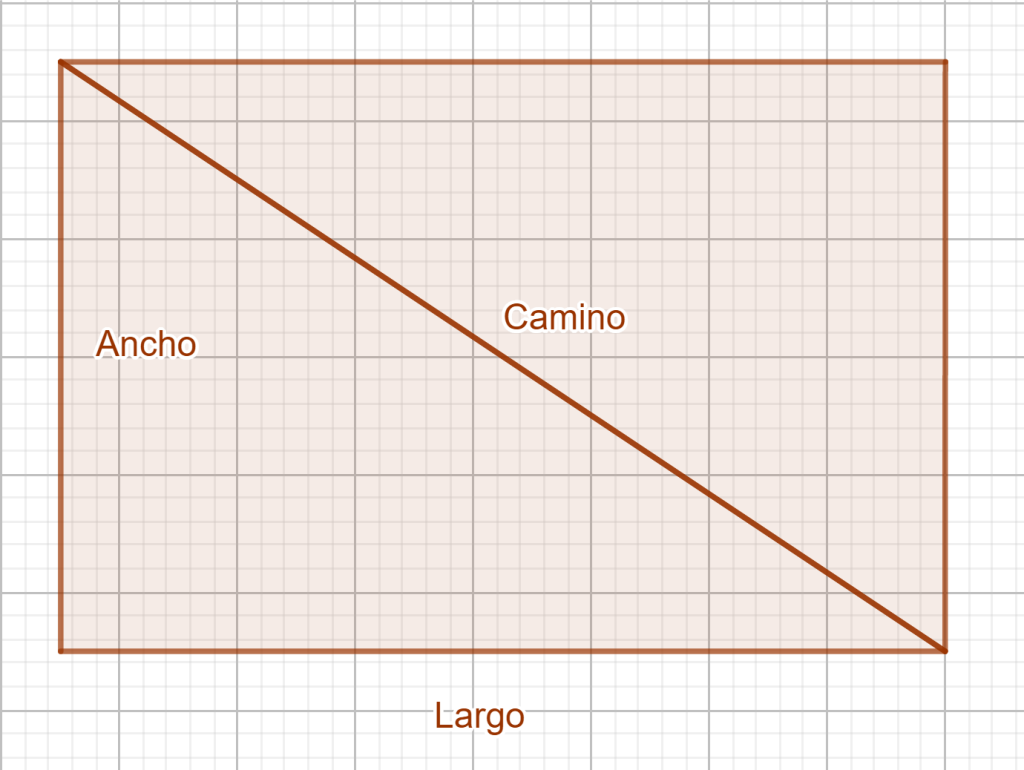
El camino que cruza a la parcela por su diagonal la divide en dos triángulos rectángulos iguales. Si nos quedamos con uno de ellos, conocemos su hipotenusa, que es el camino, y uno de los catetos (el ancho), por lo que la fórmula adecuada es la tercera:
El ancho de la parcela es, por tanto, 15 metros aproximadamente.
Intrusismo en la enseñanza de las matemáticas: una breve reflexión.
Acabo de leer una encendida discusión en un grupo de Facebook en el que participo acerca de si es apropiado o no que cualquiera que tenga una titulación universitaria compita en igualdad de condiciones con un licenciado o graduado en matemáticas para ejercer como profesor de esta materia en Secundaria y Bachillerato. En ella, algunos compañeros calificaron como «intrusismo» la proliferación de ingenieros y arquitectos en estos puestos docentes, lo que no sentó muy bien a otros, como era de esperar.
Si ánimo de extenderme sobre el asunto, me gustaría compartir con ustedes la breve reflexión que publiqué en ese mismo foro: Leer más →
Dos demostraciones sencillas para alumnos de Bachillerato
Cuando en matemáticas se hace una afirmación de cualquier tipo, como por ejemplo «el cuadrado de la longitud de la hipotenusa de un triángulo rectángulo es la suma de los cuadrados de las longitudes de sus catetos» o «si n es un número entero mayor que 2, entonces no existen números enteros x, y, z tales que 
Cuando un matemático hace un descubrimiento, lo presenta al resto del mundo siguiendo un esquema formal muy claro y bien determinado. Primero, enuncia unas hipótesis, que son una serie de condiciones previas que se sabe que son factibles, después enuncia la tesis, que es el descubrimiento en sí, y tras esto escribe la demostración de la tesis, que son una serie de razonamientos que nos llevan desde la hipótesis hasta la tesis a través de pasos que deben estar siempre bien justificados.
Por ejemplo, en el primero de los enunciados anteriores, el Teorema de Pitágoras, una forma de enunciar la hipótesis sería consideremos un triángulo rectángulo cualquiera, en el cual la hipotenusa mide a y cuyos catetos miden b y c respectivamente. La tesis sería entonces
y una demostración sería, por ejemplo, la que podemos encontrar cliqueando sobre esta figura:
(Para la segunda afirmación hay una demostración maravillosa pero no tengo espacio suficiente en esta entrada del blog). Leer más →
¿Hay partes en un metro que no se pueden medir?
****Por alguna misteriosa razón las fórmulas que ilustraban esta entrada han desaparecido en algunos navegadores, espero poder arreglarlo pronto. Mil perdones.****
En general la idea de medir no tiene mucho misterio. En nuestra vida diaria el concepto de algo que no se pueda ser medido se reduce a no tener un metro lo suficientemente largo o un reloj lo bastante preciso. Sin embargo, la Teoría de la Medida nos demuestra que existen cosas que no se pueden medir por mucho que uno intente ponerles una cinta métrica encima. Incluso podemos encontrarnos con partes del mismo metro imposibles de medir. ¿No se lo creen? Les convenceré mostrándoles este ejemplo atribuido a Hausdorff*.
Para empezar aclararemos que, en la teoría de la medida, la medida que representa el concepto que tenemos todos de lo que podemos medir con un metro es la denominada medida de Lebesgue, que en el caso de la recta real mide la distancia entre dos puntos a y b restando el menor al mayor**
Como podemos ver esta es la distancia que todos entendemos que hay entre ambos puntos.
La Ciencia y sus Demonios: A vueltas con Euromillones
Les enlazo a continuación mi entrada del viernes pasado en La Ciencia y sus Demonios en la que explico porqué es bastante fácil creer que a uno le va a tocar la lotería cuando en realidad sería más fácil ver a un político español invirtiendo en ciencia. Espero que les guste.
http://lacienciaysusdemonios.com/2013/03/15/a-vueltas-con-euromillones/
El Máquina de Turing 
Comentarios recientes